
ยินดีต้อนรับทุกท่าน เข้าสู่ เว็บแทงหวยออนไลน์ชั้นนำอันดับ 1 ของไทยที่จ่ายแพงที่สุด 2020
เว็บหวย999lucky เว็บหวยชั้นนำ ที่มีการ บริการดีเลิศ รวดเร็วทันใจ ด้วยการ การันตรีจากลูกค้าหลายๆ ท่าน เว็บเราจึงเป็นเว็บหวยนึง ที่ลุกค้าหลายๆ ท่าน ให้ความไว้วางใจด้วย การบริการมากว่า 10 ปี
ยินดีต้อนรับทุกท่าน เข้าสู่ เว็บแทงหวยออนไลน์ 999lucky เว็บหวยที่ดีที่สุด จ่ายแพง ที่สุดในประเทศตอนนี้ มีผู้คนชอบชื่นในการเล่น หวยออนไลน์ เป็นอย่างมากเลยเเละได้รับความนิยมสูงเลยทีเดียวเชียว แทงหวยเว็บหวยชั้นนำ !
ทางเว็บของเรานั้น จึงได้นำ หวยรัฐบาล หวยยี่กี หวยฮานอย หวยใต้ดิน มาให้ ลูกค้าทุกท่าน ได้เพลิดเพลิน ในการแทง เเละยังสามารถแทงผ่าน ทางเข้าหน้าเว็บ 999lucky ได้เลยทางเราขอรับรองเลยว่าทางเราจะคอยดูเเล support ลูกค้าทุกท่านเสมือนเป็นลูกค้าvipทุกคนเท่าเทียมกันอย่างแน่นอน ครับ !
แทงหวยกับเรา 999LUCKY เว็บหวยจ่ายจริง มีระบบที่ทันสมัยมากที่สุดปลอดภัย 100%
แทงหวยออนไลน์ 2020 กับเรา 999lucky จ่ายไม่ยั้ง ต้องการมั่งคั่ง ไม่รู้ตัวอย่ากลัว การแทงหวย ท่านจะได้พบกับ มิติใหม่ ของเว็บ แทงหวยออนไลน์ ที่มีการแทงที่หลากหลาย แปลกใหม่ ต่างจากเว็บอื่นๆ ท่านจะได้พบกับ มิติใหม่ของการแทงหวย อย่างนอน !
เว็บพนันหวยออนไลน์มาแรง2020 ที่ครบวงจรที่ดีที่สุด เเละได้รับการยอมรับมากที่สุดสำหรับนักเสี่ยงโชคในไทยมี หวยออนไลน์ ให้ท่านเลือกเล่นมากมาย คัดสรรค์หวยที่ดีที่สุดทั่วโลกมาให้ท่านได้เล่นกันอย่างจุใจ เเละเพลิดเพลิน ครับ สนใจสมัครแทงหวย !
และไม่ว่าจะเป็น…..หวยรัฐบาล หวยจับยี่กี หวยหุ้นไทย หวยหุ้นต่างประเทศ หวยสิงคโปร์ หวยลัคกี้เฮง หวยฮานอยเช้า หวยฮานอยบ่าย หวยฮานอยดิจิตอล หวยมาเลย์พิเศษ หวยมาเลกลันตัน หวยมาเล ดิจิตอล หวยมาเลเช้า หวยมาเลบ่าย หวยมาเล 5G หวยลาว VIP หวยลาวพิเศษ หวยลาว5D
หวยนิเคอิ Vip หวยนิเคอิ พิเศษ หวยนิเคอิ ดิจิตอล หวยฮังเส็ง Vip หวยฮังเส็งพิเศษ หวยฮังเส็งดิจิตอล เป็นต้น และยังมีเกมส์ คาสิโนออนไลน์ อีกมากมาย อาทิเช่น เสือมังกร ปั่นแปะ เป่ายิ้งฉุบ สล็อต รูเร็ต บาคาร่า และเกมส์กีฬาอื่นๆ อีกมากมาย ติดต่อ-สอบถาม !
จุดเด่นของ เว็บหวยออนไลน์ 999LUCKY คือเปิดบริการรับแทงหวยซื้อ หวยออนไลน์ชั้นนำ กับเราเพราะมีความมั่นคง ด้านการเงินปลอดภัย 100% แถมยังมี อัตราการจ่าย สูงถึงบาทละ 800 ส่วนลดเยอะจ่ายเงินแล้ว เล่นได้เงินจริง จ่ายเต็ม ไม่มีโกง แน่นอนครับ !
สำหรับ เว็บหวยออนไลน์ชั้นนำ ของเรายังเปิดบริการรับ แทงหวยลาว ทุกชนิดอีกด้วย !
- หวยลาวไกสอน พมวิหาน
- หวยลาวไชยบุรี
- หวยลาวเซกอง
- หวยลาวท่าแขก
- หวยลาวปากซัน
- หวยลาวปากเซ
- หวยลาวพงสาลี
- หวยลาวโพนสะหวัน
- หวยลาวโพนโฮง
- หวยลาวสาละวัน
- หวยลาวเมืองไซ
- หวยลาวหลวงน้ำทา
- หวยลาวหลวงพระบาง
- หวยลาวอนุวง
- หวยลาวห้วยทราย
- หวยลาวอัตตะปือ
- หวยลาวซำเหนือ
ศูนย์รวม หวยออนไลน์ ทุกชนิด จ่ายจริงจ่ายสูง ไม่มีเลขอั้น ไม่มีประวัติการโกงอย่างเเน่นอน ที่สำคัญ…ท่านจะได้พบกับ มิติใหม่ของ การแทงหวย ที่ท่านไม่เคยพบเคยเจอ มาจากเว็บหวยที่ไหน แน่นอน ครับ
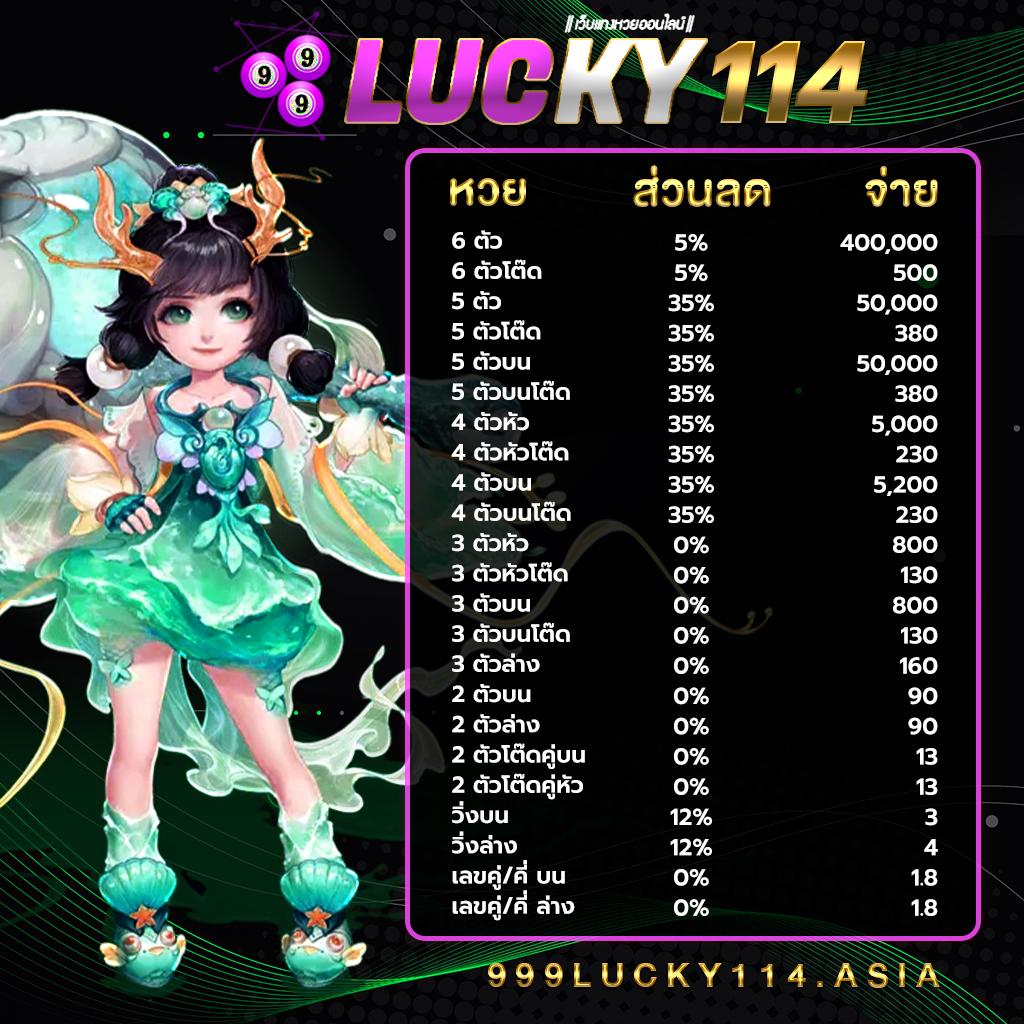
อัตตราจ่ายของทางเว็บหวยยอดนิยมอันดับหนึ่ง 999LUCKY
โปรโมชั่นหวยลดสูงสุด 33% จ่ายมากที่สุด 550 แทงหวยปลอดภัยมั่นใจ
- 3 ตัว ลดสูงสุด 33% จ่าย 550 บาท
- 2 ตัวบนและล่าง ลดสูงสุด 28% จ่าย 70 บาท
- 3 ตัวล่าง จ่าย 125 บาท
- วิ่งอัตราลด 12%3 ตัวโต๊ด จ่าย 105 บาท
- 2 ตัวโต๊ด จ่าย 12 บาท
- แทงขั้นต่ำเพียง 10 บาทเท่านั้น
สำหรับทุกท่านที่กำลังมองหา เว็บแทงหวยจ่ายเยอะ ที่จ่ายจริง ไม่โกงเเละยังมี อัตราจ่ายแพง ที่สุดในตอนนี้ เเละมีคนไทยนิยม เล่นมากที่สุด 999lucky จึงเป็นอีก 1 เว็บแทงหวยอีกนึงที่คนไทยหลายๆคน ให้ความไว้วางใจ มากที่สุด !
999LUCKY114 เว็บแทงหวยออนไลน์ชั้นนำอันดับ 1 ที่ดีที่สุด 2020
มั่นคง ปลอดภัย จ่ายจริง ไม่โกง ระบบ ฝาก-ถอน รวดเร็วทันใจ ต้องที่นี่ที่เดียวเท่านั้น
หวยรัฐบาล | หวยยี่กี | หวยฮานอย | หวยมาเลย์ | หวยออนไลน์



